DXでさらなる成長を

第二十七回  画像分類用のネットワーク構造

第十七回 では、ディープラーニング用ネットワークの構成例について説明しました。 画像分類の場合を想定しながら、少し振り返りましょう。

以下は、畳み込み層、プーリング層、全結合層を複数組み合わせたネットワークの一例です。

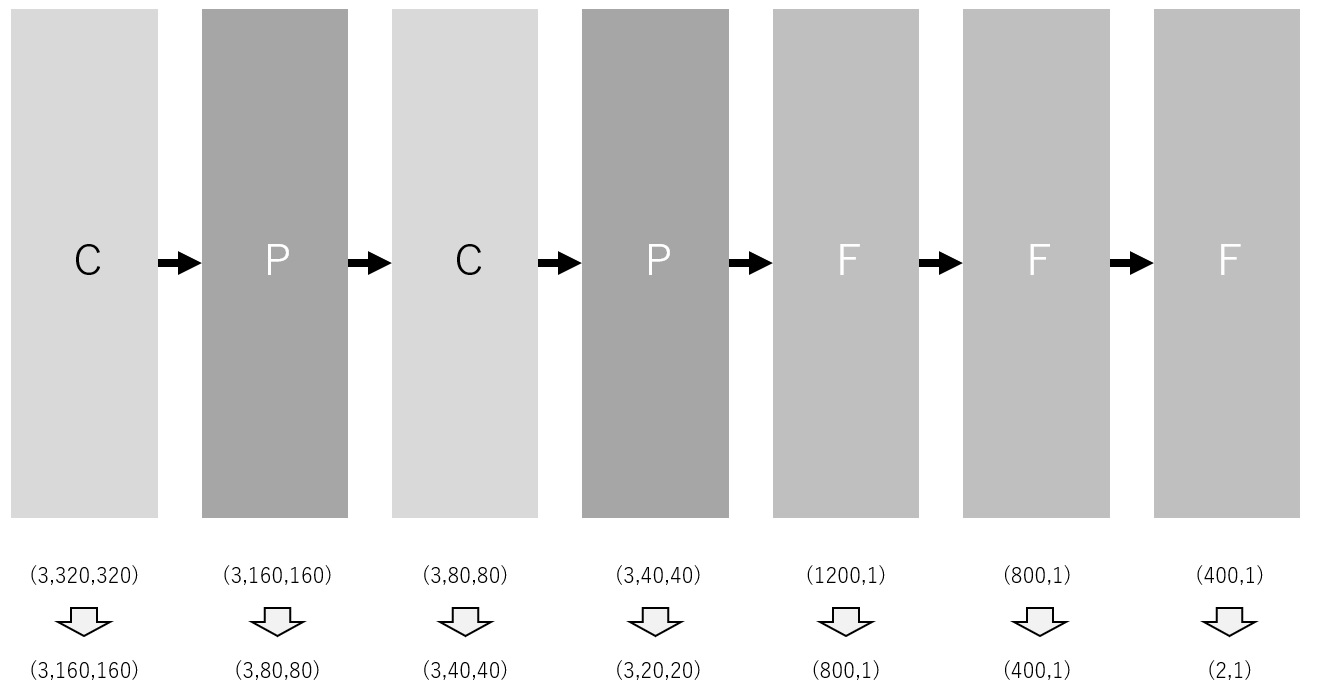
画像を入力する際に、サイズを 320×320 に調整します。 RGBの3チャンネルを想定しているため、行列サイズは (3,320,320) となっています。

最初の畳み込み層は、フィルターサイズ 2×2 、スライドサイズ 2×2 です。 したがって、出力サイズは 3×160×160 です。

二番目はプーリング層で、フィルターサイズ 2×2 、スライドサイズ 2×2 です。 したがって、出力サイズは 3×80×80 です。

同じ仕様の畳み込み層とプーリング層をあと一つずつ追加しています。 最後のプーリング層での出力サイズは 3×20×20 です。

最初の全結合層の前で、正方行列を列ベクトルに変更します。 したがって、入力行列サイズは (1200,1) です。

第十三回 で述べたとおり、各人工ニューロンにおける計算は、以下の式によって表わされます。

全結合層には、複数の人工ニューロンがあり、入出力のすべてが相互に接続されています。 最初の全結合層は、入力行列サイズが (1200,1) 、出力行列サイズが (800,1) です。 つまり、入力側の人工ニューロン数が 1200 、出力側の人工ニューロン数が 800 です。 上の式を、すべての人工ニューロンに対して行列を使用して書くと、以下のようになります。

$x$ のサイズは (1200,1) 、 $u$ のサイズは (800,1) ですから、 $W$ のサイズは (800,1200) 、 $b$ のサイズは (800,1) です。 また、 $z$ のサイズは (800,1) です。

最後の全結合層での行列サイズは、 (2,1) としています。 これは、犬と猫など、二つのクラスを認識することを想定しているからです。 四つのクラスを認識するのであれば、行列サイズは (4,1) とする必要があります。

最後の全結合層における活性化関数は、ソフトマックスとする必要があります。 これにより、出力行列の成分値を足し合わせると1となる数値を求めることができ、各クラスの確率を取得できるようになります。