第二十五回 逆畳み込み
セマンティック・セグメンテーションのような、画像を生成する人工知能を制作する場合、畳み込みによっていったんサイズを小さくした画像を、再び拡大する処理が必要になります。 逆畳み込みは、この目的で使用される計算要素です。
畳み込みの詳しい処理内容については、 第十五回 で述べましたが、ストライドとパディングについて説明していません。 逆畳み込みの説明に必要となりますので、まずはストライドから説明します。
下図は、 第十五回 で示した、グレースケール画像に対する畳み込みの処理例です。
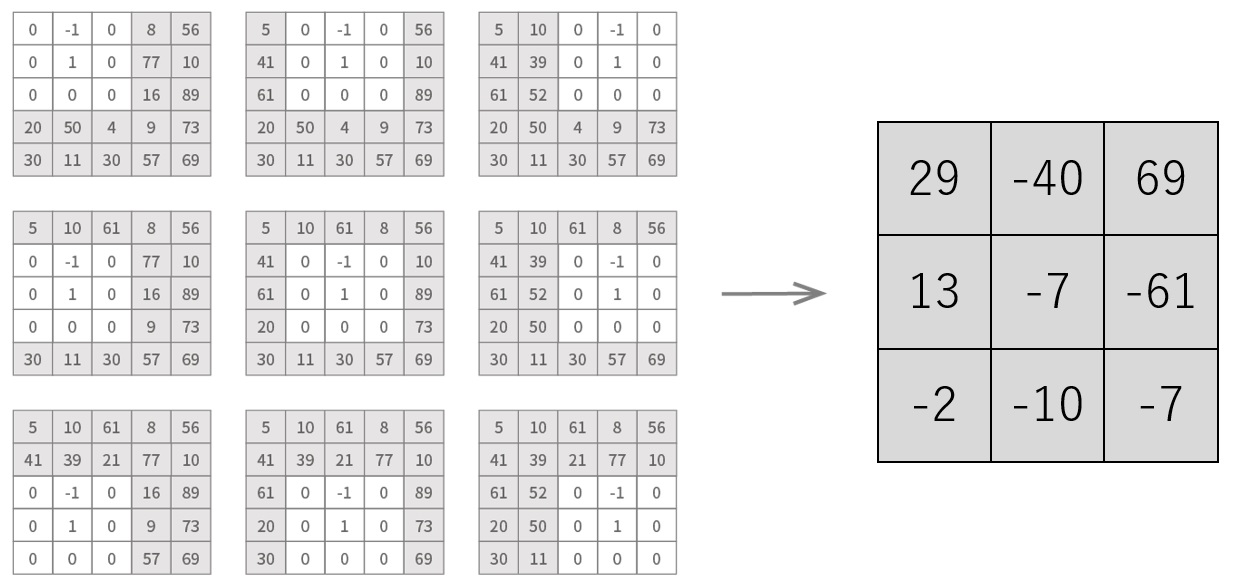
ここでは、フィルタを右および下に1ピクセルずつ移動させながら畳み込み処理を行いましたが、例えば2ピクセルずつ移動させながら処理を行うこともできます。 畳み込み処理の際にフィルタを移動させる距離のことを、ストライドと呼びます。 以下はその処理例です。
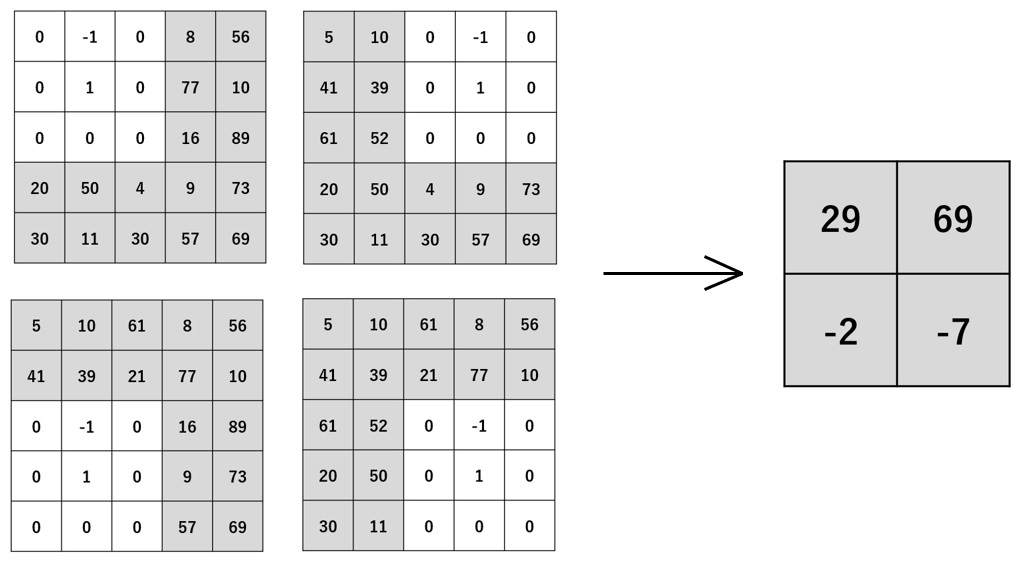
畳み込み処理の前に、画像の周囲に余白を配置することで、畳み込み結果の画像サイズを大きくすることができます。 画像の周囲に与える余白のサイズを、パディングと呼びます。 以下に、ストライド3、パディング2とした畳み込み計算例を示します。
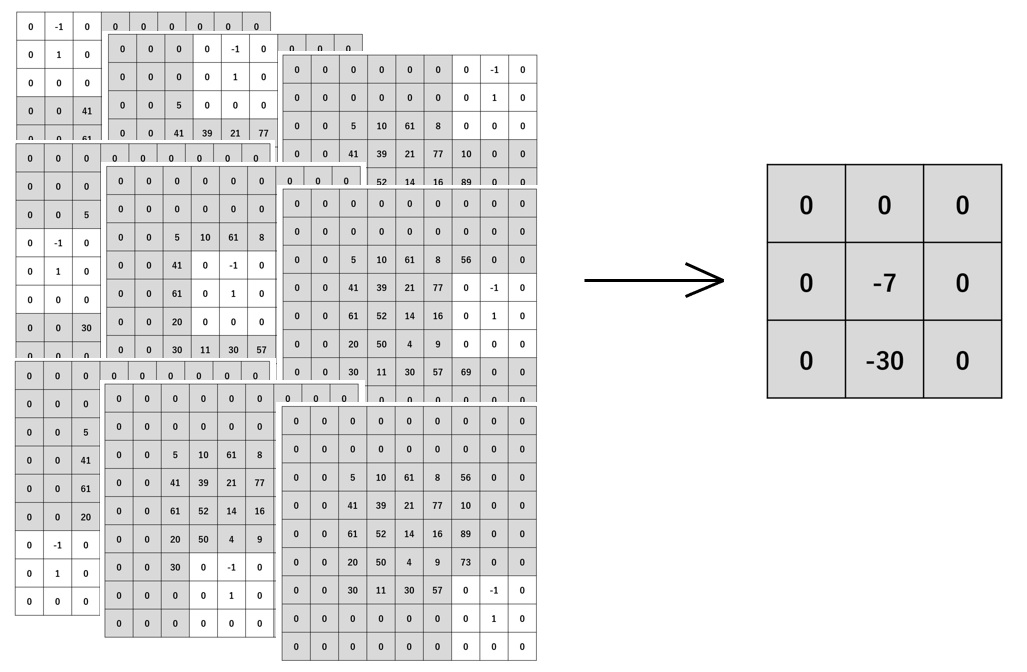
ここから、逆畳み込みについて説明します。
逆畳み込みでは、畳み込みと異なり、入力データサイズを拡大してから計算を実行します。
すでに説明したとおり、畳み込みでは、フィルタサイズ、ストライド、パディングの数値を適切に選ぶことで出力画像のサイズを変化させることができます。 逆畳み込みは、フィルタサイズ、ストライド、パディングの数値と出力画像のサイズとの関係において、畳み込みの逆となります。 しかしながら、畳み込み計算の逆を実行するわけではない点に注意が必要です。
上図の例について振り返りましょう。 入力パラメータは
入力画像サイズ : ×
フィルタサイズ : ×
ストライド : ×
パディング : ×
出力サイズは × となります。
したがって、逆畳み込みの場合、入力パラメータ
入力画像サイズ : ×
フィルタサイズ : ×
ストライド : ×
パディング : ×
に対して、出力サイズは × となります。
以下、具体的な処理内容について説明します。
(1) ストライドに従いピクセル間へ余白を追加
ストライドから1を引いた値分だけ、入力データのピクセル間に余白を追加します。 これにより、ストライド1で畳み込みと同じ処理を行うだけで、期待されるサイズの出力画像が得られます。
(2) フィルタサイズに従い入力画像周囲へ余白を追加
フィルタサイズから1を引いた値分だけ、入力データの周囲に余白を追加します。 これにより、ストライド1で畳み込みと同じ処理を行うだけで、フィルタサイズが1より大きい場合においても、期待されるサイズの出力画像が得られます。
(3) パディングに従い入力画像周囲で余白を除去
パディングの値分だけ、入力データの周囲で余白を除去します。 畳み込みにおけるパディングとは、入力データに対して余白を追加する処理です。 したがって、逆畳み込みにおいては、入力データから余白を削除することで、結果として期待されるサイズの出力画像が得られることとなります。
(4) ストライド1で畳み込みを実施
完成した入力データに対して畳み込み処理を実施します。 この際、ストライドを1とすることに注意が必要です。
文章の説明だけでは分かりにくいでしょうから、以下に具体的な例を挙げます。
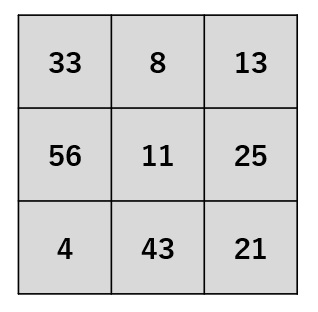
入力画像サイズを × 、フィルタサイズを × としましょう。 以下はその一例です。
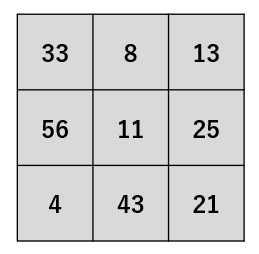 入力画像
入力画像 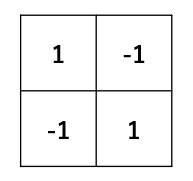 フィルタ
フィルタ ストライドとパディングについていくつか例を挙げて具体的な処理内容を見ていきます。
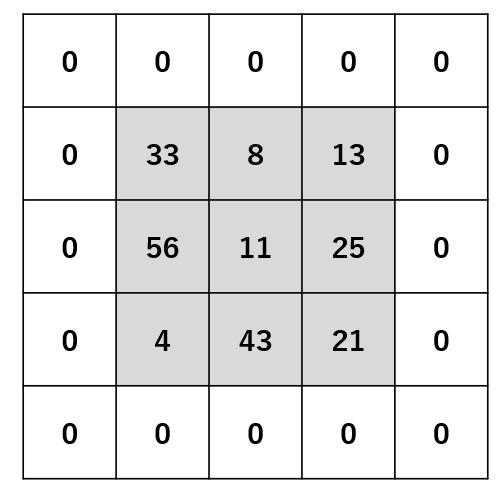
♦ ストライド=1 、パディング=0
ステップ1
ステップ2

ステップ3
->
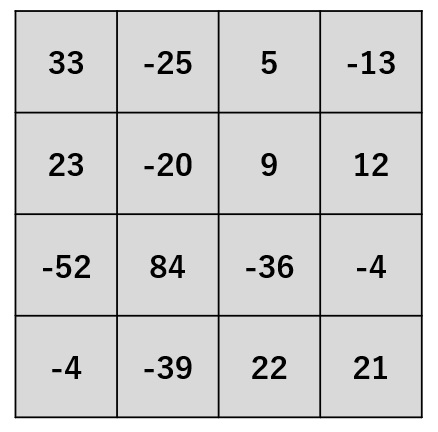 結果
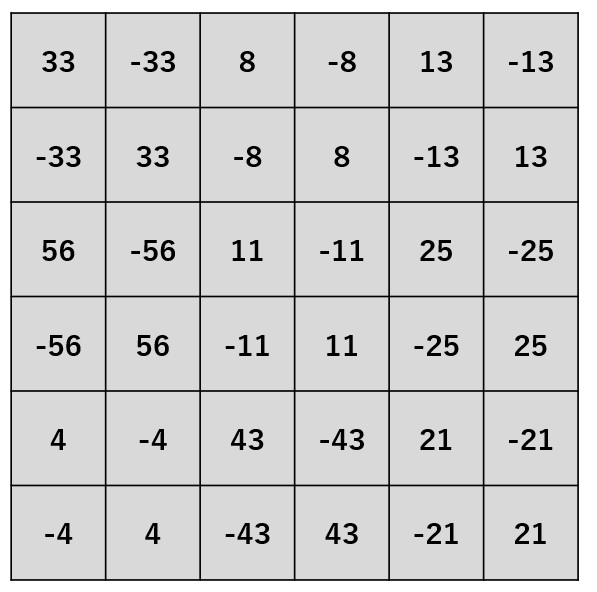
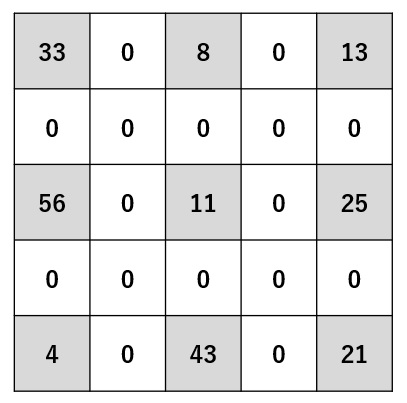
結果 ♦ ストライド=2 、パディング=0
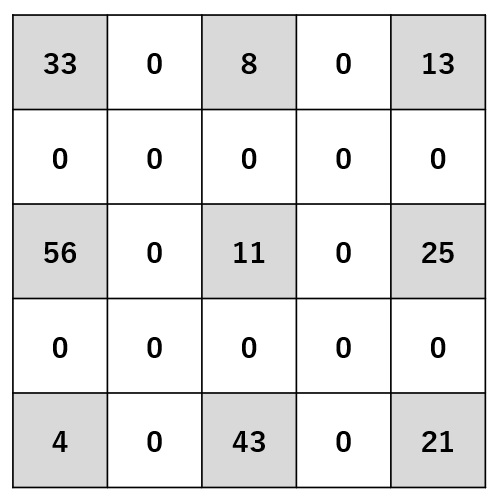
ステップ1
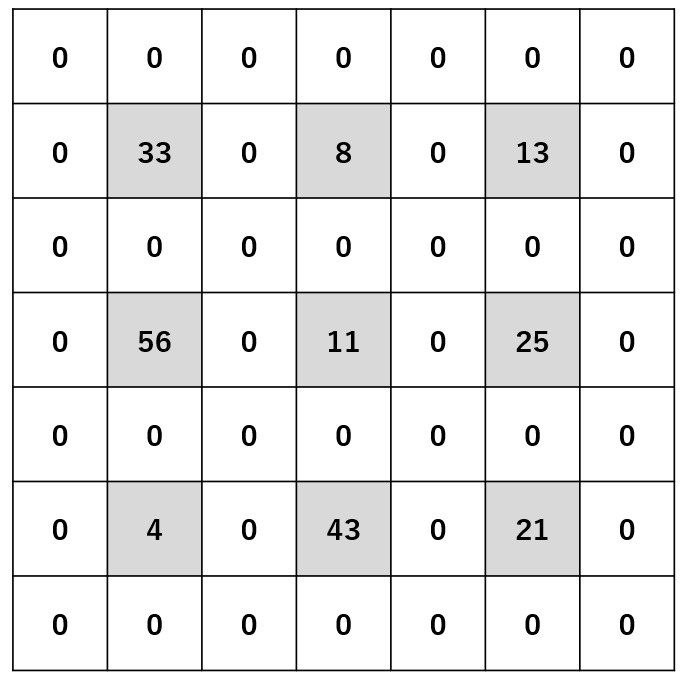
ステップ2

ステップ3
->
 結果
結果 ♦ ストライド=2 、パディング=1
ステップ1
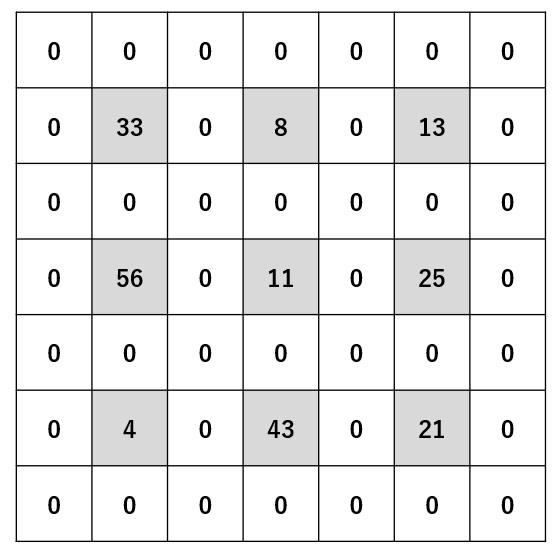
ステップ2

ステップ3
->
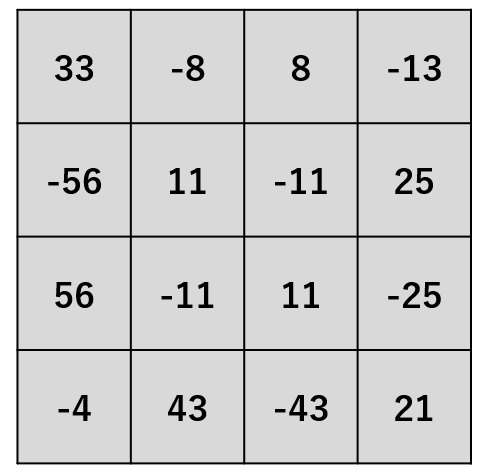 結果
結果 それぞれの例について、逆畳み込みによる出力画像を使用して畳み込みを行った場合、出力画像サイズが × となります。 このことから、前に述べた、 逆畳み込みは、フィルタサイズ、ストライド、パディングの数値と出力画像のサイズとの関係において、畳み込みの逆となります。 という事実が、確認できたと思います。
複数チャンネルの画像に対する処理は、畳み込みと同様です。 フィルターグループ数を2以上とすることで、複数チャンネルの出力画像を得ることができます。