第十八回 パラメータ推定の方法
ディープラーニングでは、複数の層を持つネットワークを構築し、入力データを与えた時の出力値と教師データとの差が、できるだけ0に近づくように、内部パラメータを調整していきます。 この作業のことをパラメータ推定と呼びます。
各人工ニューロンのパラメータを適切に調整する方法として、確率的最急降下法(Stochastic Gradient Descent, SGD)があります。
ディープラーニングの目的は、教師データに近づける方向に重みとバイアスの値を変化させることです。 以下、重みに着目しますが、バイアスについても同じ考え方が適用できます。
重みを 、教師データとの差を とするとき、 以下の更新式により重みの値を変更します。
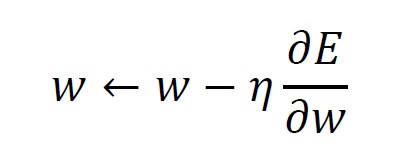
は学習率と呼ばれる値です。 を の関数ととらえ、 を勾配の負の方向に少しずらします。 この作業を繰り返すことで、勾配が0となる場所に限りなく近づいていきます。
このことを直感的に理解するため、二次関数を例に考えてみましょう。
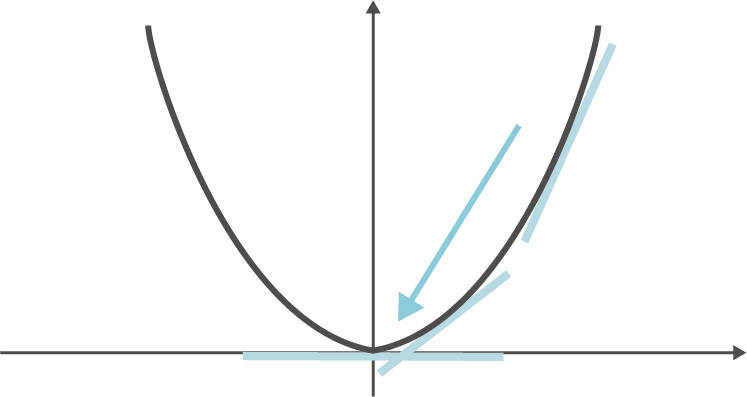
勾配が0になる点から遠い場合は、重みを大きく動かします。 一方、勾配が0になる点に近づくにつれて、重みの変更量は小さくなります。 こうして、勾配が0になる点に近づいていきます。
活性化関数は様々なものが提案されていますが、パラメータ推定が行えるよう、微分可能な関数を選ぶことが重要となります。