DXでさらなる成長を

第十九回  学習の最適化

ネットワークに対するパラメータの調整を行うにあたり、探索しようとする領域に深い谷がある場合は、谷の端で大きく値が変更され、谷からなかなか脱出できなくなります。

このような不都合を解決することを目指し、より発展したパラメータ推定法が提案されています。

モーメンタムSGDは、確率的最急降下法に慣性項を付与する手法です。 教師データとの差を $E$ 、前回の計算における重みの更新量を $\Delta w$ 、調整係数を $\mu$ とすると、下記の式を用いてパラメータを変更します。

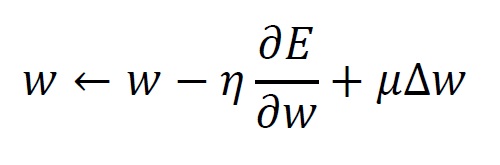
第3項は、前回の更新方向を維持しようとする働きを持っており、モーメンタム項と呼ばれます。 これにより、深い谷に入った場合に起こる確率的最急降下法の欠点を解決する効果が期待できます。

Adamは、過去の更新方向を考慮するため、勾配の移動平均を利用します。

重みを $w$ 、教師データとの差を $E$ とし、その勾配を $g$ とすると、

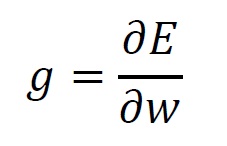
と表せます。

現在の計算ステップを $t$ とすれば、上式は以下の通り書き換えられます。

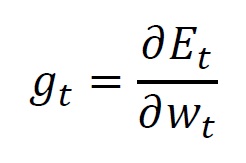
ここで、前のステップで使用した勾配の一次モーメント(平均) $m_{t-1}$ と、勾配の二次モーメント(分散) $v_{t-1}$ から、現在の計算ステップで利用する値を求めます。 式で表現すると、

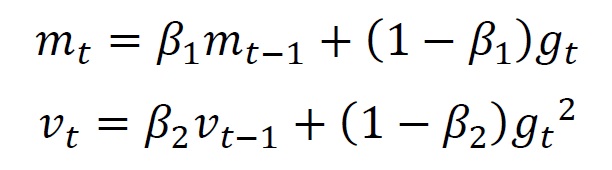
続いて、それぞれの値に対してバイアス調整を行います。詳細は関連書籍をご参照ください。

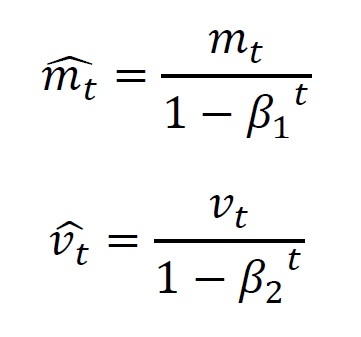
更新式は以下の通りです。

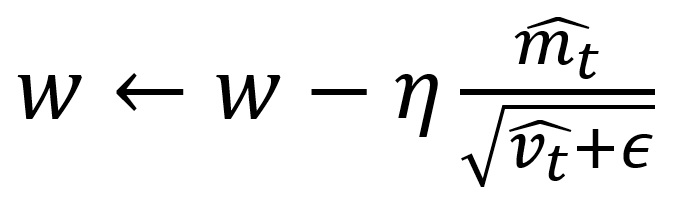
$\epsilon$ は、コンピュータ上で計算不能となることを避けるための値で、ごく小さな値を指定します。

${\beta }_1$ は0.9、 ${\beta }_2$ は0.999とすることが推奨されています。

ディープラーニングでは、畳み込みや全結合など、複数の計算ロジック要素を重ねてネットワークを構築します。 制作しようとする人工知能が複雑になり、要素の数が増えてくると、パラメータ数が膨大になり、学習が進みづらくなります。 ここで紹介したAdamは、パラメータごとに学習定数を変化させる手法であることから、特にパラメータ数が多い場合に効果的であることが知られており、昨今の論文では非常に多く目にします。