第二十九回 バッチ正規化
多数の層を持つネットワークでは、入力に近い側の層でパラメータを変更することにより、それより後方の層における入力の分布を変えてしまい、学習がうまく進まなくなることがあります。 バッチ正規化は、ミニバッチごとの入力を平均0、標準偏差1の分布に変更することで、活性化関数の飽和領域に入らないようにする手法です。
いくつかの活性化関数を例に、学習がうまく進まない事象がどのようにして起こるか見てみましょう。
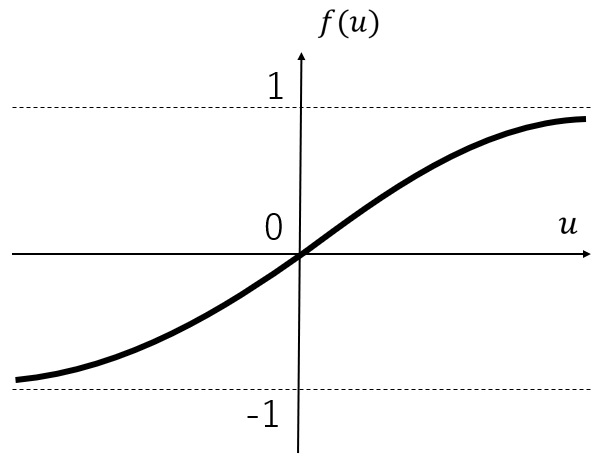
第十四回 で示した通りですが、Tanh関数のグラフは以下のようになります。
入力の分布が下図のようになっていたとしましょう。
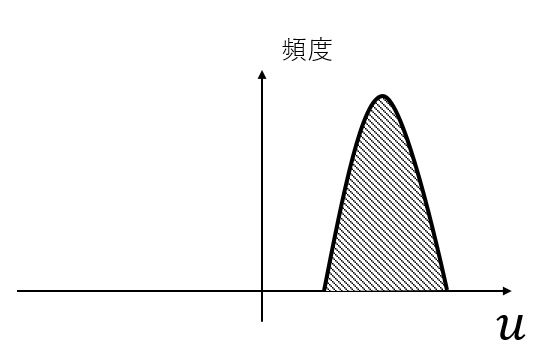
Tanhのグラフのうち、傾きが小さい領域に対応する値が多いため、重みの値を大きく変化させても、出力の値はあまり変化しません。 そこで、以下のように、平均0、標準偏差1の分布となるよう、入力値を変換します。
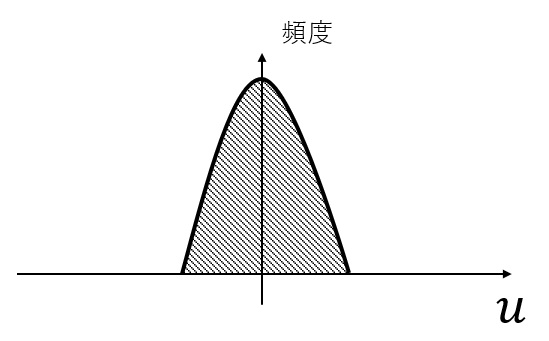
Tanhのグラフのうち、傾きが大きい領域に多くの入力が存在します。 そのため、重みと出力の値とが比較的連動しやすくなります。
第十四回 で示した通りですが、ReLU関数のグラフは以下のようになります。
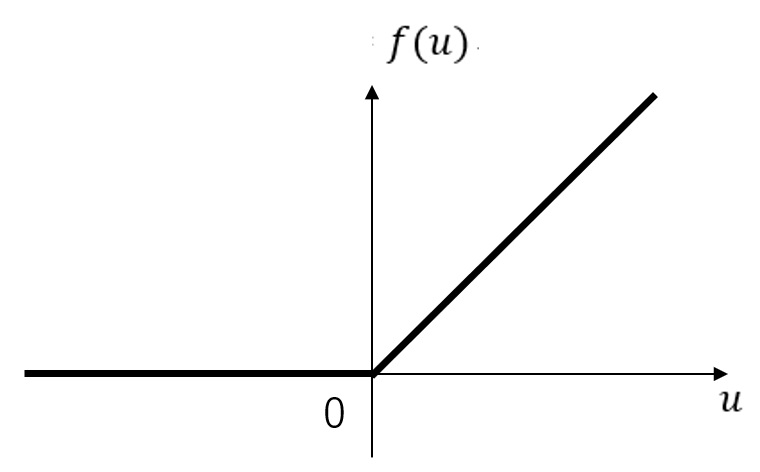
入力の分布が負の領域に偏っていたとすると、ほとんどの出力が0となってしまい、学習に参加できなくなります。 つまり、ディープラーニングを続けても、なかなか収束に至らない可能性があります。
バッチ正規化の詳しい処理内容については、かなり複雑な数式が登場するため、専門書に譲ります。 入力の数値自体を変更する処理であることから、逆伝搬でも考慮が必要で、また、その式もかなり煩雑になります。